Teams managing complex IT infrastructure are often made up of a combination of full time employees (FTE's) and contigent workers (a.k.a, contractors). Teams that have too many contractors and not enough FTE's are often ineffective. Teams that have too many FTE's and not enough contractors are effective but expensive. What is the right balance? I got to thinking whether or not I might be able to come up with an equation that could model the effectiveness of teams that are blended with FTE's and contractors and came up with a model which I'll explain as we go.
Warning: This is pseudo-science and is based on one person's observations of working with many different types of teams. Please do not take it as scientific truth.
The premise of this model is based on the curious tendency for contractors to struggle with “ownership” of complex systems. There's a correlation between how well a system is run and how many FTE's are involved. My theory is that FTE's, by nature, are more prone to owning a system “end to end” because they're in it for the long haul. They're more willing to do things outside of their job description to keep a system well maintained. For example, reaching out to stakeholders/customers and setting up meetings, thinking about system failure modes and planning mitigating strategies, re-architecting stable systems for better efficiency, etc. Contractors, on the other hand, are more prone to hitting pre-defined targets that are part of their scope of work. This is not surprising as this is exactly what they are paid to do! Contractors who act like FTE's often don't stay contractors for very long. They either get hired by their sponsoring company or they get re-assigned to another sponsor to put out some fire in another account.
All in all, I don't think there is anything wrong with this sytem as long as it is utilized effectively. A complex system needs both generals and soldiers to operate effectively. The work that contractors do is often the type of work that FTE's don't want to do and the work that FTE's do is work that contractors see as outside of their scope. Complex systems require an ownership factor that cannot be provided by contractors alone.
Therefore, in order for leadership to maintain long running, stable, cost efficient teams around complex systems they must accept these rules of nature and plan accordingly. After much thought about the fundamental truths of this system I've come up with the following conclusions:
- Contractors alone cannot own anything fully.
- When contractors outnumber FTE's things are generally bad.
- A team full of FTE's is the most effective but also the most expensive.
For example, if you had a moderately complex system that you felt could be adequately covered by 5 engineers. We'll call this 5 ownership units. Could you come up with 5 ownership units in a cheaper manner by mixing in contractors? Maybe we could optimize this sytem if we put into mathematical terms:
- An FTE can provide one full unit of ownership
- A contractor can only offer partial ownership units
- Many contractors together on their own can come close to providing full ownership but can never reach a full ownership unit.
- More FTE's “boost” contractor effectivness. In other words, contractors provide more ownership units when there are more FTE's involved.
I believe the following formula comes close to modeling how many effective headcout you can expect out of a mixed team.
Where y is the number of full time employees and x is the number of contractors
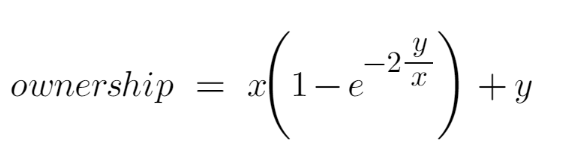
Let's break this down and examine the parts in more detail. For starters, the total effective ownership headcount should be the sum of FTE headcount plus some modifier for contractor effectiveness which can be represented as x(?) + y. So how do we determine the effectiveness? After much thought it was clear that I needed a mathmatical equation that could approach, but never be 1. It also had to be zero if there were no full time employees in the mix. In addition, it needed to be “boosted” if there was a high ratio of FTE's to contractors. Therefore this formula was used which I'm calling the “contractor coefficient” or “cc”
cc = (1-e^(-2(y/x)))
Let's look at a short data table to explain it's effect on the overall effective contractor headcount:
| y | x | cc | notes |
|---|---|---|---|
| 0 | 1 | 0 | a single lone contractor cannot provide any ownership |
| 1 | 1 | 0.86 | a 1:1 pairing of contractors to FTE's is pretty efficient |
| 5 | 10 | 0.63 | Double the number of contractors as FTE's is reasonably effective |
| 1 | 10 | 0.18 | 10x as many contractors as employees is not very efficient at all |
| 100 | 1 | 1 | As the team effectively approaches all FTE's the coefficient is effectively 1 |
| 1 | 0 | !div0 | I'm not good enough at math to fix this (if you have all FTE's then you don't need this formula anyway) |
Now that we have a decent formula for effective headcount we can easily modify it to find the total cost of ownership for different mixes:
Where j is contractor salary, k is employee salary, x is number of contractors, and y is number of employees.
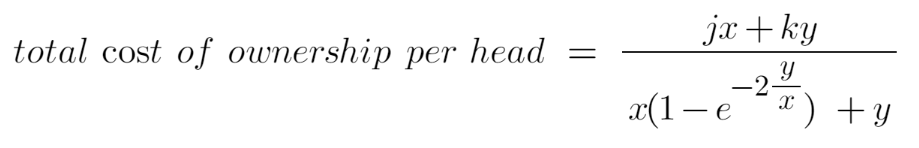
Using these two formulas, let's plug in some numbers in and examine a data table.

If we analyze the above table we can come up with an interesting conclusion.
Teams are most effective and efficient when the FTE to contractor ration is between 1:1 and 2:1 but most effective at a 5:4 ratio.
Of course, there are known limitations to this model. For one, There are some really, really good contractors out there and some really bad FTE's that can throw this off. However, those cases tend to work themselves out of organizations over time. Also, effectiveness can vary greatly by cost. Some very expensive contractors can almost be substituted as FTE's depending on how expensive they are. However, even a very very expensive contractor will only “own” so much.
I'd like to modify the equation to include considerations for quality based on price but I'll leave that as a TODO for now.
Does this ring true from your own experience? Let me know what you think.
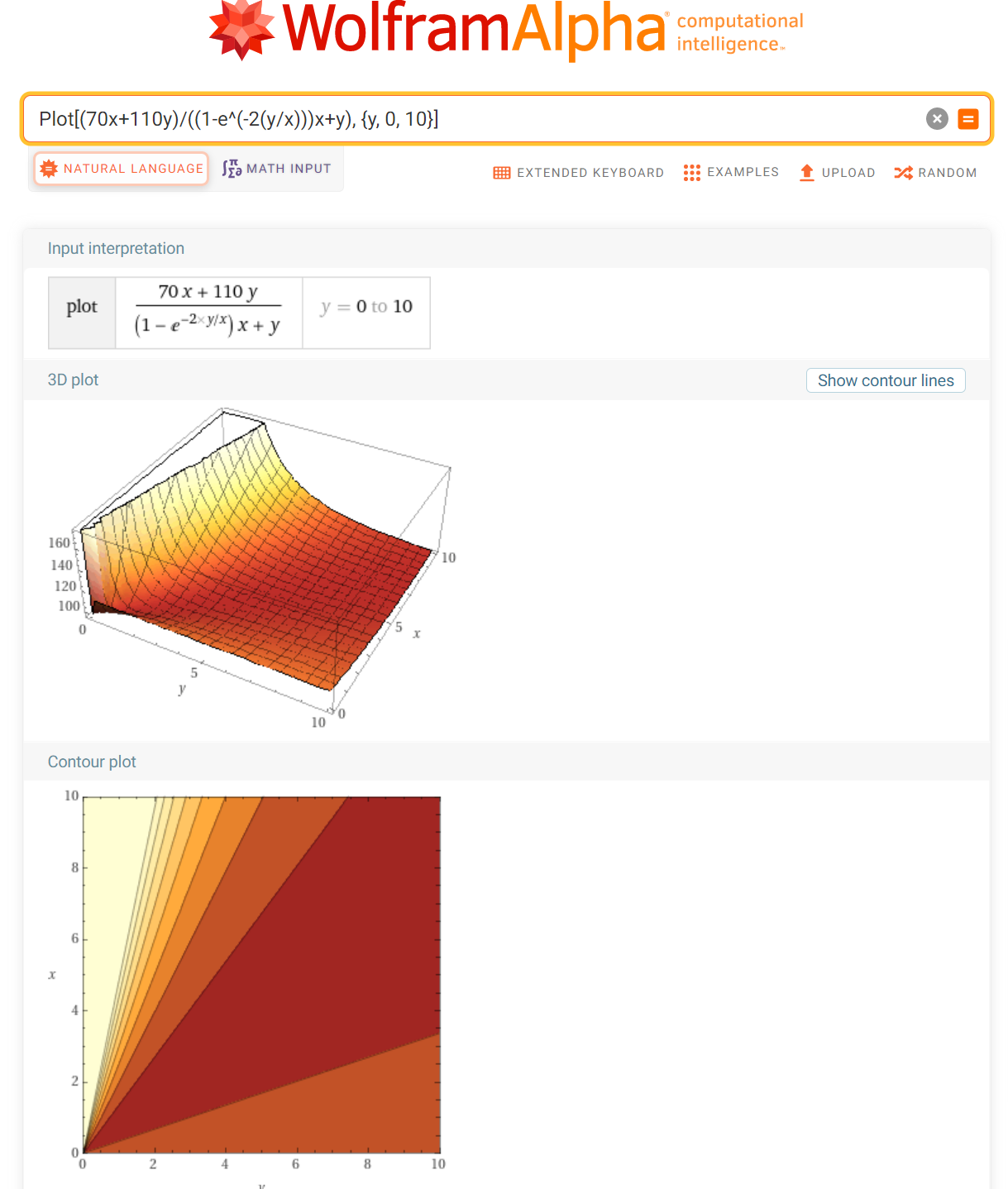
P.S. - The plot for this on Wolfram Alpha are interesting. I'd also like to solve the equation for y and x to confirm the min/max in order to determine the most effective ratio.
Plot[(70x+110y)/((1-e^(-2(y/x)))x+y), {y, 0, 10}]
Where y is number of FTE's, x is number of contractors, 110 is FTE salary in thousands of USD per year, 70 is contractor salary in thousands of USD per year
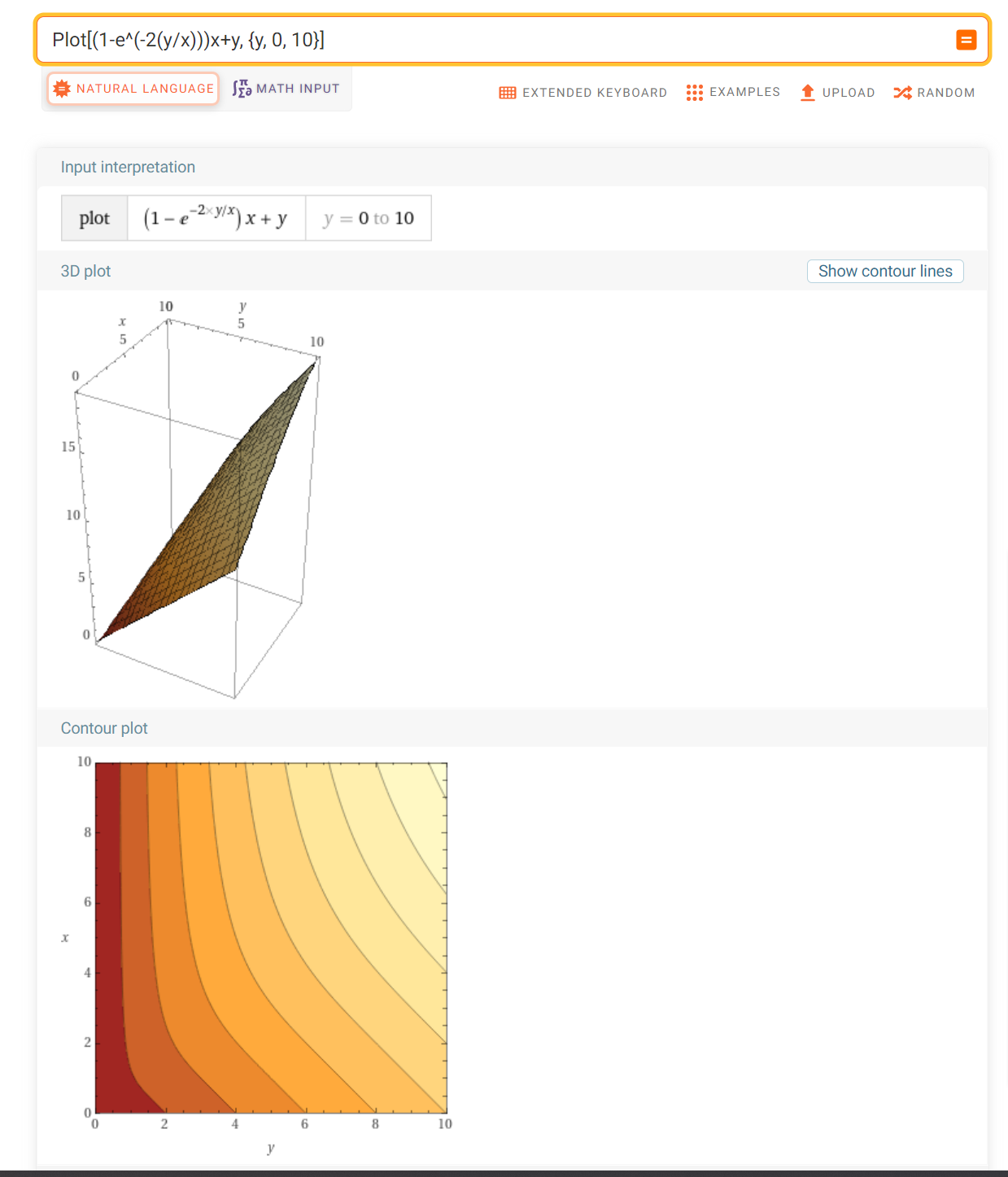
Plot[(1-e^(-2(y/x)))x+y, {y, 0, 10}]
Where y is number of FTE's, x is number of contractors
* The method for how this conclusion was reached was coming up with a rough formula to describe my observations and then plugging in headcount numbers for known real-life teams and my percieved effectiveness of those teams. If the results did not match my experience then I tweaked the formula until it matched more closely. Then I put in some extreme edge cases and made sure it still sounded sane.